题目链接:https://www.luogu.org/problemnew/show/P1074
题面:
题目描述
小城和小华都是热爱数学的好学生,最近,他们不约而同地迷上了数独游戏,好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了,于是他们向 Z 博士请教,Z 博士拿出了他最近发明的“靶形数独”,作为这两个孩子比试的题目。
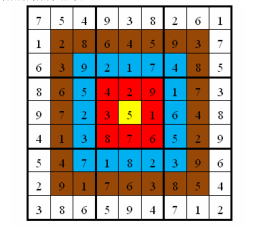
靶形数独的方格同普通数独一样,在 99 格宽×99 格高的大九宫格中有99 个 33 格宽×33 格高的小九宫格(用粗黑色线隔开的)。在这个大九宫格中,有一些数字是已知的,根据这些数字,利用逻辑推理,在其他的空格上填入 11 到 99的数字。每个数字在每个小九宫格内不能重复出现,每个数字在每行、每列也不能重复出现。但靶形数独有一点和普通数独不同,即每一个方格都有一个分值,而且如同一个靶子一样,离中心越近则分值越高。(如图)

上图具体的分值分布是:最里面一格(黄色区域)为 101 分,黄色区域外面的一圈(红色区域)每个格子为99分,再外面一圈(蓝色区域)每个格子为88 分,蓝色区域外面一圈(棕色区域)每个格子为77分,最外面一圈(白色区域)每个格子为66分,如上图所示。比赛的要求是:每个人必须完成一个给定的数独(每个给定数独可能有不同的填法),而且要争取更高的总分数。而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和
总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。如图,在以下的这个已经填完数字的靶形数独游戏中,总分数为 2829。游戏规定,将以总分数的高低决出胜负。
由于求胜心切,小城找到了善于编程的你,让你帮他求出,对于给定的靶形数独,能够得到的最高分数。
输入输出格式
输入格式:
一共 99 行。每行99个整数(每个数都在 0-9−9 的范围内),表示一个尚未填满的数独方格,未填的空格用“”表示。每两个数字之间用一个空格隔开。
输出格式:
输出共 11 行。输出可以得到的靶形数独的最高分数。如果这个数独无解,则输出整数-1。
数独的规则就是同行同列同宫1-9必填且不能重复。
我开始就是一顿无脑暴力搜索,肯定是T了,后面加了个优化,从0少的行开始搜,降低了搜索树的高度,这样的话速度快很多
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
|
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <queue>
#include <set>
#include <string>
#include <vector>
using namespace std;
#define MAXN 50000
struct length
{
int r, leng;
bool operator<(const length &l) const
{
return leng < l.leng;
}
};
int matrix[20][20] = {{0}};
length len[10];
int getScore(int r, int c)
{
if (r == 4 && c == 4)
return 10;
if ((r == 0 || r == 8) && c >= 0 && c < 9)
return 6;
if ((c == 0 || c == 8) && r >= 0 && r < 9)
return 6;
if ((r == 1 || r == 7) && c >= 1 && c < 8)
return 7;
if ((c == 1 || c == 7) && r >= 1 && r < 8)
return 7;
if ((r == 2 || r == 6) && c >= 2 && c < 7)
return 8;
if ((c == 2 || c == 6) && r >= 2 && r < 7)
return 8;
if ((r == 3 || r == 5) && c >= 3 && c < 6)
return 9;
if ((c == 3 || c == 5) && r >= 3 && r < 6)
return 9;
return 10;
}
bool check(int r, int c, int val)
{
int rt = r - r % 3;
int ct = c - c % 3;
set<int> s;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
if (matrix[rt + j][ct + i] == val)
return true;
if (matrix[i * 3 + j][c] == val || matrix[r][i * 3 + j] == val)
return true;
}
}
return false;
}
void print()
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
cout << matrix[i][j] << ' ';
}
cout << endl;
}
}
int calc()
{
int score = 0;
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
score += matrix[i][j] * getScore(i, j);
}
}
return score;
}
int maxx = 0;
int cnt = 0;
void dfs(int r, int c)
{
if (r > 8 && c > 8)
{
maxx = max(maxx, calc());
// cout << "Score: " << score << endl;
// print();
// cout << "----------------------------" << endl;
return;
}
else if (r < 9 && c > 8)
{
dfs(r + 1, 0);
}
else if (matrix[len[r].r][c] != 0)
dfs(r, c + 1);
else
{
for (int i = 1; i <= 9; i++)
{
if (matrix[len[r].r][c] == 0 && !check(len[r].r, c, i))
{
matrix[len[r].r][c] = i;
dfs(r, c + 1);
matrix[len[r].r][c] = 0;
}
}
}
}
int main()
{
// for(int i = 0; < 9; ++)
// {
// for(int j = 0; < 9; ++)
// {
// cout << getScore(i, j) << " ";
// }
// cout << endl;
// }
for (int i = 0; i < 9; i++)
{
int count = 0;
for (int j = 0; j < 9; j++)
{
cin >> matrix[i][j];
if (matrix[i][j] == 0)
count++;
}
len[i].r = i;
len[i].leng = count;
}
sort(len, len + 9);
dfs(0, 0);
cout << maxx;
return 0;
}
|
这是我第一次交的代码,T了10个点….,WA了一个点。WA的原因是没有特判无解的情况…..后来想想判断点我为啥要用set…直接遍历就好了嘛….
我就把check函数改成了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
bool check(int r, int c, int val)
{
int rt = r - r % 3;
int ct = c - c % 3;
set<int> s;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
if (matrix[rt + j][ct + i] == val)
return true;
if (matrix[i * 3 + j][c] == val || matrix[r][i * 3 + j] == val)
return true;
}
}
return false;
}
|
并特判了无解的情况,还是T了,不过这次只T了6个点,说明还是可以的…
check的O(N)查询还是有点高,于是我又用了2个二维数组把他降低到了O(1)…空间换时间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
|
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <queue>
#include <set>
#include <string>
#include <vector>
using namespace std;
struct length
{
int r, leng;
bool operator<(const length &l) const
{
return leng < l.leng;
}
};
int matrix[12][12] = {{0}};
int row[12][12] = {{0}};
int col[12][12] = {{0}};
length len[10];
int getScore(int r, int c)
{
if (r == 4 && c == 4)
return 10;
if ((r == 0 || r == 8) && c >= 0 && c < 9)
return 6;
if ((c == 0 || c == 8) && r >= 0 && r < 9)
return 6;
if ((r == 1 || r == 7) && c >= 1 && c < 8)
return 7;
if ((c == 1 || c == 7) && r >= 1 && r < 8)
return 7;
if ((r == 2 || r == 6) && c >= 2 && c < 7)
return 8;
if ((c == 2 || c == 6) && r >= 2 && r < 7)
return 8;
if ((r == 3 || r == 5) && c >= 3 && c < 6)
return 9;
if ((c == 3 || c == 5) && r >= 3 && r < 6)
return 9;
return 10;
}
bool check(int r, int c, int val)
{
int rt = r - r % 3;
int ct = c - c % 3;
if (row[r][val])
return true;
if (col[c][val])
return true;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
if (matrix[rt + j][ct + i] == val)
return true;
}
}
return false;
}
void print()
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 0; j++)
{
cout << matrix[i][j] << ' ';
}
cout << endl;
}
}
int calc()
{
int score = 0;
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
score += matrix[i][j] * getScore(i, j);
}
}
return score;
}
int maxx = 0;
void dfs(int r, int c)
{
if (r > 8)
{
maxx = max(maxx, calc());
// cout << "Score: " << score << endl;
// print();
// cout << "----------------------------" << endl;
return;
}
else if (c > 8)
{
dfs(r + 1, 0);
}
else if (matrix[len[r].r][c])
dfs(r, c + 1);
else
{
for (int i = 1; i <= 9; i++)
{
if (!check(len[r].r, c, i))
{
matrix[len[r].r][c] = i;
row[len[r].r][i] = 1;
col[c][i] = 1;
dfs(r, c + 1);
matrix[len[r].r][c] = 0;
row[len[r].r][i] = 0;
col[c][i] = 0;
}
}
}
}
int main()
{
for (int i = 0; i < 9; i++)
{
int count = 0;
for (int j = 0; j < 9; j++)
{
cin >> matrix[i][j];
if (matrix[i][j] == 0)
count++;
else
{
row[i][matrix[i][j]] = 1; //第i行的matrix[i][j]
col[j][matrix[i][j]] = 1; //第j列的matrix[i][j]
}
}
len[i].r = i;
len[i].leng = count;
}
sort(len, len + 9);
dfs(0, 0);
if (maxx == 0)
maxx = -1;
cout << maxx;
return 0;
}
|
提交之后还是T了一个点,宫的查询还是O(N)….
于是我又加了一个数组,把宫的查询也变成了O(1)…这次只T了一个点…
(于是我+了O2优化…假装自己过了…
在计算那里,还是可以边搜边加分数,既然已经过了,我就没想改了…

